Prove that (5.6.15) is a solution to the diffusion equation (5.6.14) with the initial condition n(x(vector), 0) = (x(vector)). Show that it conserves the total

Prove that (5.6.15) is a solution to the diffusion equation (5.6.14) with the initial condition n(x(vector), 0) = δ(x(vector)). Show that it conserves the total number of particles.

What is the full width at half maximum of this distribution as a function of time?

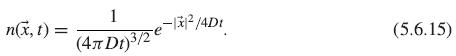
n(x, t) = 1 (4 Dt)3/2ex/4D1 (5.6.15)