(a) Show that the following is a solution to the diffusion equation (3.71) for particles in a homogeneous infinite medium:

so N is the total number of particles. Note that this is a Gaussian distribution with width σ = √4Dt. Plot this solution for several values of σ. In the limit as t → 0, the particles are all localized at the origin. As time passes, they random-walk (diffuse) away from the origin, traveling a mean distance ασ = α√4Dt after time t, where α is a coefficient of order one.

(b) Suppose that the particles have an arbitrary initial distribution n_o(x) at time t = 0. Show that their distribution at a later time t is given by the following Green’s function integral:

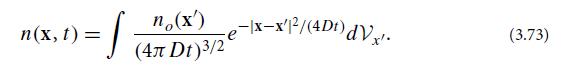
(c) What form does the solution take in one dimension? And in two dimensions?

n = N (4 Dt) 3/20 -r/(4Dt) (3.72)