Question: Show that if a band has a minimum but is not isotropic, that is, that the density of states near k(vector) = 0 is still

Show that if a band has a minimum but is not isotropic, that is,E = Eo + Ak + Bk + Ck,

that the density of states near k(vector)  = 0 is still proportional to √(E − E0). In this case, the Taylor expansion is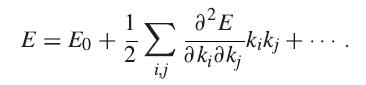

This gives a matrix for the quadratic term, which can always be diagonalized.

E = Eo + Ak + Bk + Ck,

Step by Step Solution

★★★★★

3.44 Rating (167 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Since the energy can be expanded around its minimum as 1 8 E 24 OkiOkj E Eo and the o... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Solid State Physics Essential Concepts Questions!

Q:

1. Anne and Billy are playing a simple dice game. Each rolls one die and the one with higher number wins if the higher number is at least two more than the lower number. If the numbers are the same,...

Q:

Show that if a random variable has a uniform density with the parameters and , the rth moment about the mean equals (a) 0 when r is odd; (b) 1 / r + 1 ( / 2)r when r is even.

Q:

A persymmetric matrix is a matrix that is symmetric about both diagonals; that is, an N N matrix A = (aij) is persymmetric if aij = aji = aN+1i,N+1j, for all i = 1, 2, . . . , N and j = 1, 2, . . ....

Q:

The experimental result differs from the assumption. The result shows that the ring oscillator frequencies can be grouped into two groups, where the first group is the high frequency group for the...

Q:

E-Physics Tutorial Book Note: I have attached below the lesson for the 3 activities. Thank you so much for your time and effort. Activity 1. Directions: Use the right-hand rule to determine the...

Q:

IOE 419 Mark S. Daskin Service Operations Management IOE Department Winter, 2017 University of Michigan Problem set 4 DUE: MONDAY - February 20, 2017 Points: 100 points total Problem 1: Babette has...

Q:

PLEASE COMPLETE NO LATER THAN 10/07 @8:00AM Each question(1,2,& 3) must be a minimum of 200 words. Please make answers detailed and knowledgeable based off the attached reading. ARE YOU ABLE TO...

Q:

Please see attachment. All three question need to be answered in narrative format. If you have questions, just let me know. Normal requirement for references are 2 outside our course text....

Q:

Jones & Bartlett Learning, LLC. NOT FOR RESALE OR DISTRIBUTION CHAPTER Hot Spot Analysis 10 LEARNING OBJECTIVES C A R R Provide a working definition of a \"hot spot.\" , Be able to explain different...

Q:

Consider the following context-free grammar of expressions E ::= n | (E, E) where n ranges over integers. (a) Present a right-most derivation of the expression ((21, 18), 17). [2 marks] (b) List the...

Q:

Sexual harassment should not be tolerated at the workplace. Workplace romances are a natural occurrence in organizations. Are both of these statements true? Can they be reconciled?

Q:

Listed below are the numbers of years it took for a random sample of college students to earn bachelors degrees (based on data from the National Center for Education Statistics). Construct a 90%...

Q:

What is the difference between an object and an objective case pronoun? Provide examples of each.

Q:

1.S In the observing of a desired experimental effect example of Section 1.2 of this chapter, which interpretation of the data seems most appropriate to you? Why?

Q:

Identify the product of the following reaction: Br Br ONa 2 NaBr C4H3O2 Nao

Q:

When trans-1-phenylpropene is treated with bromine, some syn addition is observed. Explain why the presence of a phenyl group causes a loss of stereospecificity. Br + En Br2 En Br Br Syn addition...

Q:

For each of the following cases, read the curved arrows and identify which arrow-pushing pattern is utilized: a. b. c. d. e. f. g. h. i. :Ci: -0-H - 0-H 0:0-I :O:

Q:

Early distributions (before age 5912) from a traditional IRA, Roth IRA, or other qualified retirement plan are subject to a 10% penalty on the taxable part of the distribution. However, there are...

Q:

Please correct the fields which are labeled wrong. 1. Each partner receives an annual salary allowance of $55 per billable hours worked. 2. Interest is credited to the partners' capital accounts at...

Q:

Marlow Company purchased a point of sale system on January 1 for $5,400. This system has a useful life of 10 years and a salvage value of $400. What would be the depreciation expense for the second...