Show that the exact relation between density and average interparticle spacing is given by

and not simply r̄ = n^−1/3, as is often assumed. To do this, first define Q(r)dr as the probability that the nearest neighbor of a particle lies between r and r+dr, and P(r) as the probability of there being no neighbor closer than r,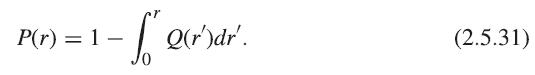 

If n is the average density of the particles, it follows that

that is, the product of the probability of no particle up to r, times the probability of a particle being between r and r + dr. Show that the mean distance between particles is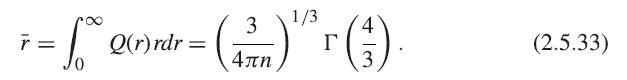

This exercise was orginally suggested by Ridley (1988).

r = 0.554n-1/3 (2.5.30)