Verify the statement above, that a hydrostatic stress leads to a hydrostatic strain, using the cubic (but not necessarily isotropic) compliance tensor deduced in part (a) of the prior exercise. Is it also the case that a pure shear stress leads to a pure shear strain?

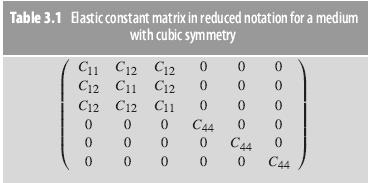
Table 3.1 Elastic constant matrix in reduced notation for a medium with cubic symmetry C11 C12 C12 C11 C120 C12 C11 0 0 0 0 0 C12 C12 0 0 0 0 0 0 0 0 0 C44 0 0 0 0 0 0 C44 0 C44 0 0