For let (Me)² mean that given a Mealy machine, an input string is processed and then the output string is immediately fed into the machine (as input) and reprocessed. Only this second resultant output is considered the final output of (Me)². If the final output string is the same as the original input string, we say that (Me)² has an identity property. Symbolically, we write (Me)² = identity.

Let Me₁ be the identity Mealy machine that looks like this:

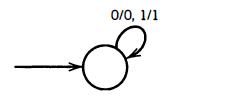
Let Me₂ be the 1's complement Mealy machine pictured below :

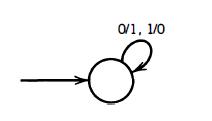
Prove that both (Me₁)² and (Me₂)² have the identity property that the result of processing any bit string is the original string again.

Transcribed Image Text:

0/0, 1/1