(a) Write a function to generate multivariate normal random numbers of a specified dimension and with a specified covariance matrix. The first statement for an \(\mathrm{R}\) function should be rmulvnorm The R function chol computes the transformation matrix from Sigma. (The function rmulvnorm has the same functionality as the function rmvnorm in the mvtnorm package.)

(b) Use your function from the previous step to generate a sample of 1,000 trivariate normal random variables with mean of 0 and variance-covariance matrix \[ \Sigma=\left[\begin{array}{rrr} 9 & -3 & 2 \\ -3 & 4 & -1 \\ 2 & -1 & 1 \end{array}\right] \]
Now, produce three bivariate contour plots of each pair of variates. This is similar to the two plots in Figure 2.8.

Figure 2.8:

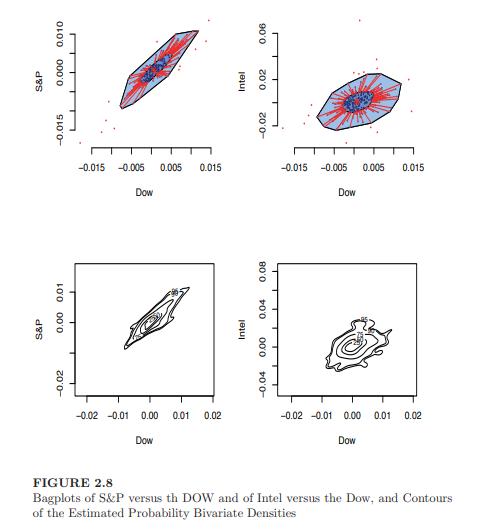
-0.02 S&P 0.00 0.01 -0.02 -0.01 0.00 0.01 0.02 Dow S&P -0.015 0.000 0.010 -0.015 -0.005 0.005 Dow Intel -0.04 0.00 0.04 0.08 FIGURE 2.8 Bagplots of S&P versus th DOW and of Intel versus the Dow, and Contours of the Estimated Probability Bivariate Densities -0.02 -0.01 0.00 0.01 0.02 Dow Intel -0.02 0.02 0.06 0.015 -0.015 -0.005 0.005 0.015 Dow