A Young's interference experiment is performed in the geometry shown in Fig. 5-14p. The pinholes are circular and have finite diameter \(\delta\) and spacing \(s\). The source has bandwidth \(\Delta v\) and mean frequency \(\bar{v} . f\) is the focal length of the lens. The following two effects cause the fringes to be attenuated away from the optical axis:

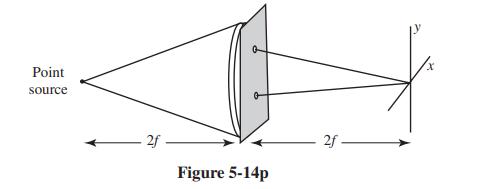
(a) The finite size of the pinholes, 

(b) The finite bandwidth of the source.

Given \(\delta, s\), and \(f\), how small must the fractional bandwidth \(\Delta v / \bar{v}\) be to assure that effect

(a) dominates over effect (b)?

Point source 2f Figure 5-14p 2f-