An ergodic real-valued random process (U(t)) with autocorrelation function (Gamma_{U}(tau)=left(N_{0} / 2 ight) delta(tau)) is applied to the input of a linear, time-invariant filter with

An ergodic real-valued random process \(U(t)\) with autocorrelation function \(\Gamma_{U}(\tau)=\left(N_{0} / 2\right) \delta(\tau)\) is applied to the input of a linear, time-invariant filter with impulse response \(h(t)\). The filter output \(V(t)\) is multiplied by a delayed version of \(U(t)\), forming a new random process \(Z(t)\), as shown in Fig. 3-3p. Show that the impulse response of the filter can be determined from measurements of \(\langle z(t)angle\) as a function of delay \(\Delta\).

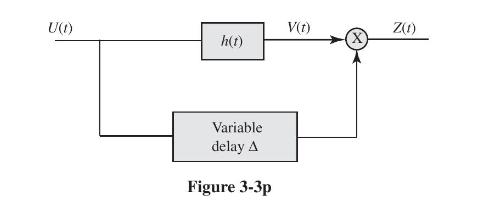
U(t) h(t) Variable delay A Figure 3-3p V(t) Z(1)