Let the real-valued random process U ( t ) U ( t ) be defined by U ( t ) = A cos ( 2

Let the real-valued random process $U\left(t\right)$ be defined by

$$U\left(t\right)=A\cos (2\pi vt-\Phi )$$

where $v$ is a known constant, $\Phi$ is a random variable uniformly distributed on $(-\pi ,\pi ),A$ is a random variable that takes on the values 1 and 2 with equal probabilities of $1/2$, and $A$ and $\Phi$ are statistically independent.

(a) Calculate the time average  for a sample function with amplitude 1 and a sample function with amplitude 2.

(b) Calculate $\overline{u^2}$.

(c) Show that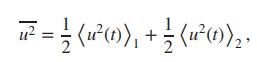
where $\text{Extra left or missing right}$ and $\text{Extra left or missing right}$ are the results of part (a) for amplitudes of 1 and 2 , respectively.

(u(t))