For our running Example 2. 2 we can use (2.53) to derive a large-sample approximation of the

Question:

For our running Example 2.

2 we can use (2.53) to derive a large-sample approximation of the pointwise variance of the learner \(g_{\mathscr{T}}(\boldsymbol{x})=\boldsymbol{x}^{\top} \widehat{\boldsymbol{\beta}}_{n}\). In particular, show that for large \(n\)

\[ \mathbb{V} \operatorname{ar} g_{\mathscr{T}}(\boldsymbol{x}) \simeq \frac{\ell^{*} \boldsymbol{x}^{\top} \mathbf{H}_{p}^{-1} \boldsymbol{x}}{n}+\frac{\boldsymbol{x}^{\top} \mathbf{H}_{p}^{-1} \mathbf{M}_{p} \mathbf{H}_{p}^{-1} \boldsymbol{x}}{n}, \quad n \rightarrow \infty \]
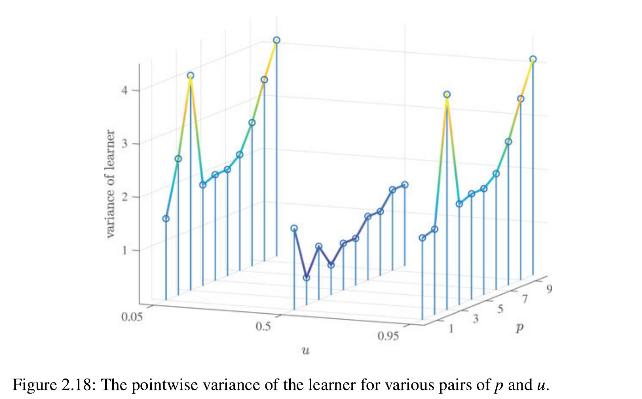
Figur 2.

18 shows this (large-sample) variance of the learner for different values of the predictor \(u\) and model index \(p\). Observe that the variance ultimately increases in \(p\) and that it is smaller at \(u=1 / 2\) than closer to the endpoints \(u=0\) or \(u=1\). Since the bias is also larger near the endpoints, we deduce that the pointwise mean squared error (2.21) is larger near the endpoints of the interval \([0,1]\) than near its middle. In other words, the error is much smaller in the center of the data cloud than near its periphery.

image text in transcribed