For a standard normal random variable z, find P(1.2, z,1.96). Find the value .025 z with area .025 to its right.

1. Name columns C1 and C2 of a MINITAB worksheet as “x,” and “P(X,5x),” respectively.

Then enter the two values for x (1.2 and 1.96) in the first two cells of column C1.

To generate cumulative probabilities for these two values, select Calc ➤ Probability Distributions ➤ Normal and the Dialog box shown in Figure 6.24 will appear.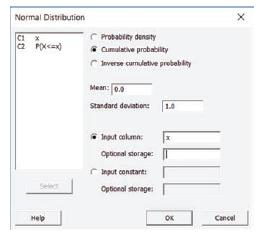

2. By default, MINITAB chooses m 50 and s 51 as the mean and standard deviation of the standard normal z distribution, so you need only to enter the Input column (C1) and make sure that the radio button marked “Cumulative probability” is selected. If you do not specify a column for “Optional storage,” MINITAB will display the results in the Session window, as shown in Figure 6.25(a).

3. To find P(1.2, z,1.96), remember that the cumulative probability is the area to the left of the given value of z. Hence, P(1.2, z,1.96)5P(z,1.96)2P(z,1.2)50.97500220.88493050.090072.
You can check this calculation using Table 3 in Appendix I if you wish!
4. To calculate inverse cumulative probabilities, select Calc ➤ Probability Distributions ➤ Normal, and click the radio button marked “Inverse cumulative probability,” shown in Figure 6.24. We need a value .025 z with area .025 to its right, or area .975 to its left. Enter .975 in the box marked “Input constant” and click OK. The value of .025 z will appear in the Session window, as shown in Figure 6.25(b). This value, when rounded to two decimal places, is the familiar 1.96 .025 z 5 used in Example 6.7

Normal Distribution C1 x 2 ) Probability density Cumulative probability Inverse cumulative probability Help Standard deviation: 1.0 Input column Optional storage: Input constant: Optional storage: Cancel