Let X 1 , . . . , X n be a simple random sample from a N(μ, Ï 2 ) population. For any constant

Let X₁, . . . , X_nbe a simple random sample from a N(μ, σ²) population. For any constant k > 0, define

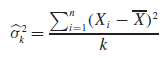
Consider σ̂²_k as an estimator of σ².

a. Compute the bias of σ̂²_k in terms of k. The sample variance s² is unbiased, and σ̂²_k = (n ˆ’ 1)s²/k.]

b. Compute the variance of σ̂²_k in terms of k. σ² s² = 2σ⁴/(n ˆ’ 1), and σ̂²_k= (n ˆ’ 1)s²/k.]

c. Compute the mean squared error of σ̂²_k in terms of k.

d. For what value of k is the mean squared error of σ²_k minimized?

(X; - (-. o = k