Let X and Y be two continuous random variables with joint probability density f(x, y) The joint distribution function F(a, b) is defined as follows Verify each of the following a F ( , ) F( , y) F(x, ) 0 b F (, ) 1 c If a 2 a 1 and b 2 b 1 ,then F (a 2 , b 2 ) F (a 1 , b 2 ) F (a 2 , b 1 ) F (a 1 , b 1 ) F(a, b) P(X s a, Y s b) f(x, y) dy dx 3D

Question: Let X and Y be two continuous random variables with joint probability density f(x, y). The joint distribution function F(a, b) is defined as follows:

Let X and Y be two continuous random variables with joint probability density f(x, y). The joint distribution function F(a, b) is defined as follows:

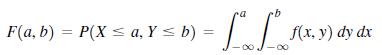
F(a, b) = P(X s a, Y s b) = f(x, y)

Verify each of the following:

a. F (-∞, -∞) = F(-∞, y) = F(x, -∞) = 0

b. F (∞, ∞) = 1

c. If a₂≥ a₁ and b₂ ≥ b₁ ,then F (a₂, b₂) - F (a₁, b₂) ≥ F (a₂, b₁) - F (a₁, b₁).

F(a, b) = P(X s a, Y s b) = f(x, y) dy dx %3D

Step by Step Solution

★★★★★

3.49 Rating (156 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To verify each of the statements we will use the properties of the joint probability density function PDF and the cumulative distribution function CDF ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Statistics For Engineering And The Sciences Questions!

Let X and Y be two continuous random variables with joint density f(x, y). Show that f 2( y x)f 1 (x) = f 1 (x y)f 2 (y)

Let X and Y be two continuous random variables defined over the unit square. What does c equal if fX,Y (x, y)=c(x2 + y2)?

Let X and Y be independent continuous random variables with respective hazard rate functions X(t) and Y(t), and set W = min(X,Y). (a) Determine the distribution function of W in terms of those of X...

Let X and Y be two continuous random variables with joint probability density function f(x, y) = 12 5 xy(1 + y) for 0 ? x ? 1 and 0 ? y ? 1, and f(x, y) = 0 otherwise. a. Find the probability P 1 4 ?...

(From MS 6.18) Find the numerical value of c to 4 decimal places. 6.18 Let X and Y be two continuous random variables with joint probability density Ice-( xty) if O s x 05 12 3 .02 09 07 10 A 08 01...

Let X and Y be two continuous random variables with joint probability density functionf(x,y) = 12/5xy(1+y) for 0 ?x ?1 and 0 ? y ? 1 Find the probability P(1/4 ? X ?1/2, 1/3 ? Y ? 2/3). Determine the...

please show step by step explanations. Thank you. 3) Let X and Y be two continuous random variables, with joint probability density function: f ( x, y )=- 9 10 x y for Ox

Let X and Y be two continuous random variables with joint probability density function (PDF) fx, x(2, y) = 6xy 0 0. (b) Find fx (x) and fy (y). (c) Are X and Y independent? (d) Find the conditional...

6. Let X and Y be two continuous random variables with joint probability density function p(x, y) = c [x + =] for 0

6. a) Consider the reaction N2(8) + 3H2(g) 2NH3(g) AHxn -92.6 kJ If 2 moles of N2 reacts with 6 moles of H2 to form NH3, calculate the work done (in joules) against the pressure of 1 atm at 25 C ?...

Consider the signal s (t) shown in Figure. (a) Determine the impulse response of a filter matched to this signal and sketch it as a function of rime. (b) Plot the matched filter output as a function...

Discuss TWO (2) strategies 1. Multi-Currency Accounts & 2. 3. Localized Revenue Streams for the foreign exchange that impact ZUS Coffee's pricing and profitability in different international markets...

Let My People Surf. The philosophy of Yvon Chouinard, not only an accomplished climber but also a passionate surfer, is that you have to surf when the surfs up. At Patagonia, workers set their own...

16. Answer parts (a) (f) of Exercise 15 with X lecture time past the hour given in Exercise 5.

17. Let X have a uniform distribution on the interval [A, B]. a. Obtain an expression for the (100p)th percentile. b. Compute E(X), V(X), and X. c. For n a positive integer, compute E(Xn ).

18. Let X denote the voltage at the output of a microphone, and suppose that X has a uniform distribution on the interval from 1 to 1. The voltage is processed by a hard limiter with cutoff values .5...

1. Calculate the expected return for Stock A. 2. Calculate the expected return for Stock B. 3. Calculate the standard deviation of Stock A. 4. Calculate the standard deviation for Stock B. Consider...

A pension fund manager is considering three mutual funds. The first is a stock fund, the second is a long-term government and corporate bond fund, and the third is a T-bill money market fund yields a...

Refer to Figure 15.1. Which lists the prices of various Microsoft options. Use the data in the figure to calculate the payoff and the profit/loss for investments in each of the following July 2017...