Refer to the IHS Journal of Hydraulic Engineering (September 2012) study of water pipes susceptible to breakage, Exercise 10.31. Recall that civil engineers used simple linear regression to model y = the ratio of repair to replacement cost of commercial pipe as a function of x = the diameter (in millimeters) of the pipe. Obtain the regression residuals and construct two graphs: (1) a plot of the residuals against diameter of the pipe, and (2) a normal probability plot. What do these plots suggest about the validity of the assumptions on the random error term?

Data from Exercise 10.31

Refer to the IHS Journal of Hydraulic Engineering (September 2012) study of water pipes susceptible to breakage, Exercise 10.8. Recall that civil engineers used simple linear regression to model y =  the ratio of repair to replacement cost of commercial pipe as a function of x = the diameter (in millimeters) of the pipe. Are the engineers able to conclude (at α = .05) that the cost ratio increases linearly with pipe diameter? If so, provide a 95% confidence interval for the increase in cost ratio for every 1 millimeter increase in pipe diameter.

Data from Exercise 10.8

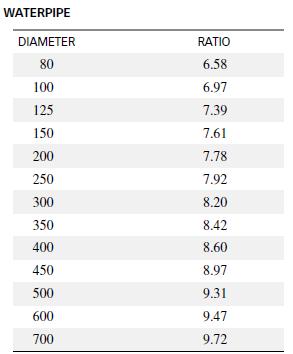
Pipes used in a water distribution network are susceptible to breakage due to a variety of factors. When pipes break, engineers must decide whether to repair or replace the broken pipe. A team of civil engineers used regression analysis to estimate y = the ratio of repair to replacement cost of commercial pipe in the IHS Journal of Hydraulic Engineering (September 2012). The independent variable in the regression analysis was x = the diameter (in millimeters) of the pipe. Data for a sample of 13 different pipe sizes are provided in the table.

Transcribed Image Text:

WATERPIPE DIAMETER RATIO 80 6.58 100 6.97 125 7.39 150 7.61 200 7.78 250 7.92 300 8.20 350 8.42 400 8.60 450 8.97 500 9.31 600 9.47 700 9.72