The probability generating function P(t) for a discrete random variable Y is defined to be P(t) =

Question:

The probability generating function P(t) for a discrete random variable Y is defined to be

P(t) = E(t^Y) = p_o+ p₁t + p₂t²+ .....

where p_{i =}P(Y = i).

a. Find P(t) for the Poisson distribution. Write

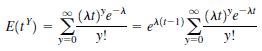
and note that the quantity being summed is a Poisson probability with mean λt.

b. Use the facts that

to derive the mean and variance of a Poisson random variable.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For answer-question

Statistics For Engineering And The Sciences

ISBN: 9781498728850

6th Edition

Authors: William M. Mendenhall, Terry L. Sincich

See More Books

Question Posted: Apr 09, 2021 02:16 PM

See More Questions

A discrete random variable x can assume five possible values: 20, 21, 22, 23, and 24. The following Minitab histogram shows the likelihood of each value. a. What is p(22)? b. What is the probability...
A discrete random variable x can assume five possible values: 2, 3, 5, 8, and 10. Its probability distribution is shown here: a. What is p(5)? b. What is the probability that x equals 2 or 10? c....
For a discrete random variable that is Poisson distributed with (= 2.0, determine the following: a. P(x = 0) b. P(x = 1) c. P(x 3) d. P(x 2)
One persons reform in some cases may be considered an attack on another persons vital interests. Describe how the antebellum reform movementsparticularly temperance, colonization, and womens...
Apple's iPod has been the portable MP3-player of choice among many gadget enthusiasts. Suppose that Apple has a constant marginal cost of 4 and that market demand is given by Q = 200 - 2P. a) If...
You hear someone comment that any inventory is a sign of waste. Do you agree or disagree? Can managers simultaneously justify holding inventories and still seek out ways to lower inventory levels?
Which of the following is an activity not usually associated with forensic accounting and fraud examination consulting and litigation support? 1. A. Assessing fraud risk associated with internal...
(Kellogg's) acquired 75% of the outstanding stock of Wholesome & Hearty Foods ("Wholesome") at the end of 2007, for cash and stock totaling $120 million. Assume that Wholesome's assets and...
Display Oracle database employee last_name and salary for employee_ids between 100and 102. Include a third column that divides each salary by 1.55 and rounds the result two decimal places.
Lakeland-Bering Aircraft Company is preparing a contract proposal to submit to the defense department for a new military aircraft, the X-300J jet fighter. Part of the proposal is a development and...
Let c be a constant and consider the density function for the random variable Y: a. Find the value of c. b. Find the cumulative distribution function F(y). c. Compute F(1). d. Compute F(.5). e....
Let Y be a geometric random variable. Show that E(Y) = 1/P . Write Thus, Then use the fact that (The sum of this infinite series is given in most mathematical handbooks.)] E(Y) = PEyq"- where q = 1 -...
How do shareholders in a publicly traded firm actually reap cash flow returns from their ownership? Who has control over which of these returns?
PLEASE ANSWER EACH QUESTION 1 Thru 4 1. Question The productivity of a resource in influenced by all but which one of the following? Select one: a. Resources prices. b. Productivity of other...
The cost of a chiropractor's services qualifies as a medical deduction. True False
Assume the following information: Percent Complete Milling Department Units Materials Conversion Beginning work in process inventory 200 40% 30% Units started into production during March 6,200 Units...
Calculate the amount of the missing item in each of the following independent cases (hint: refer to the Statement of Change in Equity): Equity, January 1 Owner's investments during the year Profit...
Prepare a vertical analysis of the income statement data for Oriole Corporation for both years. ( Net sales Cost of goods sold Gross profit Operating expenses Net income $ $632,300 456,600 175,700...
Compound A will not undergo a ring-opening reaction under thermal conditions, but compound B will. Explain. B A.
What are the three kinds of research types? Explain each type.
Of n1 randomly selected male smokers, X1 smoked filter cigarettes, whereas of n2 randomly selected female smokers, X2 smoked filter cigarettes. Let p1 and p2 denote the probabilities that a randomly...
Suppose a certain type of fertilizer has an expected Yield per acre of 1 with variance 2, whereas the expected Yield for a second type of fertilizer is 2 with the same variance 2. Let S21 and S22...
Consider a random sample X1, ... , Xn from the pdf f (x; ) = .5(1 + x) - 1 x 1 where - 1 u 1 (this distribution arises in particle physics). Show that ^ = 3is an unbiased estimator of .
Common stock value-Constant growth McCracken Roofing, Inc., common stock paid a dividend of $1.11 per share last year. The company expects earnings and dividends to grow at a rate of 4% per year for...
What would be the main feature of your plan to reintroduce Flexit to the European market again? Which one of the 4international strategies should they adopt?
A rabbit population doubles every 6 months. If the colony starts with 500 rabbits, how long will it take to reach 1500, assuming exponential growth?

The probability generating function P(t) for a discrete random variable Y is defined to be P(t) =

Question:

Eり - Se y=0 y! 一A』 !! y=0 y!

Step by Step Answer:

a The probability generating function PGF for a Poisson distributio...View the full answer

Statistics For Engineering And The Sciences

Students also viewed these Engineering questions