Question: Consider a random phenomenon specified by the probability density function (with p known) For any random sample ( X u ...,X n) from this let

Consider a random phenomenon specified by the probability density function (with p known)

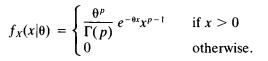
fx(x|0) = (p) 0 exp-1 if x > 0 otherwise.

For any random sample ( X u ...,X n) from this let us define X n by

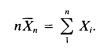
image text in transcribed

(a) Show that

image text in transcribed

is an unbiased, consistent, sufficient estimator of 0 .

(b) Find the efficiency of the most efficient estimator of 0 .

fx(x|0) = (p) 0 exp-1 if x > 0 otherwise.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Statistics For Engineers And Scientists Questions!

Q:

Hi, math experts. I am recently learning from Pattern Recognition and Machine Learning, Chris Bishop. Please provide a detailed explainations briefly for the following sections. 1. Section 1.2.2...

Q:

A random sample of size 12 is drawn from a random phenomenon specified by the probability density function with p = 16 and 0j > 0 and a second random sample of size 15 is drawn from another random...

Q:

Let X j,..., X n be a random sample of size n from a random phenomenon specified by the probability density function Find the most powerful test of size 0.05 of H0: 8 = 80, (3 = p0 against H x: 8 =...

Q:

Let Yj,...,Y5 denote the order statistics of a random sample of size 5 from a random phenomenon specified by the probability density function Show that Y2/ Y 4 and Y4 are independent random...

Q:

Let X {,..., X n be a random sample of size n from a random phenomenon specified by the probability density function Find the most powerful test of (a) / / 0- 0 = 2 against H x\ 0 = 4; (b) H {): 0 =...

Q:

Question 2 (1 point) Consider a random variable _\\ with the following probability density function: e - ac fx (20 ) = if x 2 0 elswhere Let us define the random variable Y by Y = ex Find the pdf of...

Q:

5 Consider the success run chain in Example 8.2.16. Suppose that the chain has been running for a while and is currently in state 10. (a) What is the expected number of steps until the chain is back...

Q:

ChE 697 Statistical Methods in Chemical Engineering Final Exam l. The BirnbaumSaunders distribution was devised as a means to model the lifetime of engineered products subjected to cyclic...

Q:

PSTAT W120A, Summer 2016 Assignment 3.B Due Monday Aug. 22 Directions: Please write up your solutions and submit them on GauchoSpace by the end of the day on Monday. We prefer the submission to be...

Q:

Problem #01 (8 points). Let Y,Y, ,Y be a random sample from the exponential distribution with pdf as follows (a) (4 points) Show that @ = Y is a consistent estimator of e. (b) (4 points) Obtain the...

Q:

On the basis of the following data, (a) journalize the adjusting entries at December 31, the end of the current fiscal year, and (b) journalize the reversing entries on January 1, the first day of...

Q:

The retained earnings account has a credit balance, and credit entries are used to record increases in this account. Explain why expense accounts (which are transferred to retained earnings when they...

Q:

Here is the condensed 2 0 2 1 balance sheet for Skye Computer Company ( in thousands of dollars ) : 2 0 2 1 Current assets$ 1 , 4 0 0 Net fixed assets 2 , 6 0 0 Total assets$ 4 , 0 0 0 Accounts...

Q:

a. The United States Congress is well qualified to debate and set generally accepted accounting principles. Comment. b. Speculate on why these bills were directed to amend the Securities Exchange Act...