Question: (a) Test the hypothesis that (mu_{1} eq mu_{2}) at the (alpha=0.1) level of significance for the given sample data. (b) Construct a 95% confidence interval

(a) Test the hypothesis that \(\mu_{1} eq \mu_{2}\) at the \(\alpha=0.1\) level of significance for the given sample data.

(b) Construct a 95\% confidence interval for \(\mu_{1}-\mu_{2}\).

(c) Test the hypothesis that \(\sigma_{1}>\sigma_{2}\) at the \(\alpha=0.1\) level of significance for the given sample data.

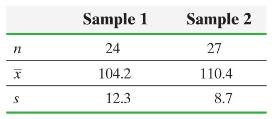
Sample 1 Sample 2 24 27 x 104.2 110.4 S 12.3 8.7

Assume that the populations are normally distributed and that independent sampling occurred.

Sample 1 Sample 2 24 27 x 104.2 110.4 S 12.3 8.7

Step by Step Solution

★★★★★

3.44 Rating (170 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Given data Sample 1 n124 x 1 1042 and s1123 sample 2 n227 x 2 1104 and s287 a Hypothesis test for mu... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Statistics Informed Decisions Using Data Questions!

Q:

(a) Test the hypothesis that \(\mu_{1} eq \mu_{2}\) at the \(\alpha=0.1\) level of significance for the given sample data. (b) Construct a \(90 \%\) confidence interval for \(\mu_{1}-\mu_{2}\). (c)...

Q:

Test the hypothesis that µ1 > µ2 at the α = 0.01 level of signiï¬cance for the given sample data. Assume that the populations are normally distributed and that...

Q:

The following samples are observations taken from the same elements at two different times: a. Assume that the populations are normally distributed and construct a 90% confidence interval for the...

Q:

19.25 19.25 19.25 19.435 19.435 19.435 19.66 19.66 19.66 20.04 20.04 20.04 20.76 20.76 20.76 19.25 20.76 19.435 20.04 19.435 20.04 0.5 1 1.5 0.5 1 1.5 0.5 1 1.5 0.5 1 1.5 0.5 1 1.5 1 1 0.5 0.5 1.5...

Q:

Please do it fast The local government of country X is committed to curb the consumption of tobacco among youngsters owing to its severe health effects. Previous attempts to regulate tobacco...

Q:

please help! The local government of country X is committed to curb the consumption of tobacco among youngsters owing to its severe health effects. Previous atiempts to regulate tobacco consumption...

Q:

1. Rhino viruses typically cause common colds. In a test of the effectiveness of echinacea, 32 of rhe 46 subjects treared with echinacea developed rhinovirus infections. In a placebo group, 44 of the...

Q:

please answer asap. will give thumbs up Use the following to answer question 4: It is believed that the average numbers of hours spent studying per day (HOURS) during undergraduate education should...

Q:

Run Markdown NFL Play-by-play Modeling and Classification In [10] : import os import pandas as pd import numpy as np import seaborn as sb import statsmodels . api as sm import sklearn. tree as tr...

Q:

Run an Anderson-Darling test for normaly Standard deviation and mean Figure Out the data and mean method of simply Histogram median simple based t owe on & APA form stigure out the data Methode of...

Q:

During 2013 and 2014, Cook Co. completed the following transactions relating to its bond issue. The companys fiscal year ends on December 31. 2013 Mar. 1 Issued $200,000 of eight-year, 6 percent...

Q:

Find the trigonometric Fourier series for a periodic signal x(t) given by, -9 -7 -3 -5 -1 10 1.0 1 3 LA 5 7 9 11 t

Q:

If many individuals recognize the same arbitrage opportunity, and sell euros forward just as you did, this would place upward pressure on the forward rate. This would continue until the premium on...

Q:

Determine the costs of these services or outputs.

Q:

Find the exact value of the expression. Do not use a calculator. cot -1 (-1)

Q:

Find the exact value, if any, of each composite function. If there is no value, say it is not defined. Do not use a calculator. sin -1 [sin(3/8)]

Q:

Find the exact value, if any, of each composite function. If there is no value, say it is not defined. Do not use a calculator. cos -1 [cos(3/4)]

Q:

Question 6 5 pts Pollo Inc.'s 5.57% bonds have a YTM of 12.31%. The estimated risk premium between the company's bonds and stocks is 4%. Pollo's cost of common equity, Re, is ____%. Round your final...

Q:

Write a program that will accepts two integers. The two integers represent the dividend and divisor of the program. Compute and display the quotient and remainder.

Q:

5. You work for a furniture store. You normally sell a living room set for $4,000 and finance the full purchase price for 24 monthly payments at 24% APR. You are planning to run a zero-interest...