The Elephant Memory Chip Co. (EMC for short) instructs its resident statistician to investigate the operating-life characteristics of their new 4 gigabyte memory chip in order to provide product information to potential buyers. The population distribution of operating lives can be specified as some exponential family distribution. The statistician intends to draw a random sample of 10,000 chips from EMC's production and apply a nondestructive test that will determine each chip's operating life. He then intends to use the outcome of the random sample to provide estimates of both the mean and variance of the chip's operating life. He needs your help in answering a few statistical questions.

(a) Letting \(\theta\) represent the unknown parameter in the exponential population distribution, what is the distribution of the sample mean, \(\bar{X}_{n}\) ? What is the mean and variance of this distribution? Does \(\operatorname{plim}\left(\bar{X}_{n}ight)=\theta\) ?

(b) The outcome of the random sample resulted in the following two outcomes:

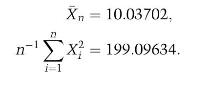
Operating life is measured in \(1,000 \mathrm{~h}\) units.

(Side Note: These are actual outcomes based on a simulation of the random sample outcome using a specific value of \(\theta\).)

The statistician uses \(\bar{X}_{n}\) to estimate the mean life, \(\theta\), of the chips. He is considering using either \(\bar{X}_{n}^{2}\) or \(S_{n}^{2}=\sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}ight)^{2} /(n-1)\) to estimate the variance, \(\theta^{2}\), of operating lives. She asks the following questions regarding the characteristics of \(X_{n}^{2}\) and \(S_{n}^{2}\) : (show your work)

(a) Does \(\mathrm{E}\left(\bar{X}_{n}^{2}ight)=\theta^{2}\) ? Does \(\mathrm{E}\left(S_{n}^{2}ight)=\theta^{2}\) ?

(b) Does \(\lim _{n ightarrow \infty} \mathrm{E}\left(\bar{X}_{n}^{2}ight)=\theta\) ? Does \(\lim _{n ightarrow \infty} \mathrm{E}\left(S_{n}^{2}ight)=\theta^{2}\) ?

(c) Does plim \(\left(\bar{X}_{n}^{2}ight)=\theta^{2}\) ? Does plim \(\left(S_{n}^{2}ight)=\theta^{2}\) ?

(d) Define asymptotic distributions for \(\left(\bar{X}_{n}^{2}ight)\) and \(\left(S_{n}^{2}ight)\). Based on their asymptotic distributions, would you recommend the use of one random variable over the other for generating an estimate of \(\theta^{2}\) ? Why or why not?

(e) Calculate the outcomes of both \(\left(\bar{X}_{n}^{2}ight)\) and \(\left(S_{n}^{2}ight)\).

(Note: The actual value of \(\theta=10\), and thus the actual value of \(\theta^{2}=100\).)

(f) The statistician has an idea he wants you to react to. He doesn't like the fact that \(\mathrm{E}\left(\bar{X}_{n}^{2}ight) eq \theta\) (that is what you found-isn't it?). He wants to define a new random variable, \(Y_{n}=a_{n}\left(\bar{X}_{n}^{2}ight)\), for an appropriate sequence of numbers \(\left\{a_{n}ight\}\), so that \(\mathrm{E}\left(Y_{n}ight)=\theta^{2}, \forall n\). Can he do it? How? If he (and you) can, then use the appropriate outcome of \(Y_{n}\) to provide another estimate of \(\theta^{2}\) ? Is it true that \(\operatorname{plim}\left(Y_{n}ight)=\theta^{2}\) ?

Transcribed Image Text:

n = 10.03702, n='\x = 199.09634. =