968 The Dominant Pole Approximation When a transform Fs has widely separated poles, then those closest to the j-axis tend to dominate the response because

9–68 The Dominant Pole Approximation When a transform FðsÞ has widely separated poles, then those closest to the j-axis tend to dominate the response because they have less damping. An approximation to the waveform can be obtained by ignoring the contributions of all except the dominant poles. We can ignore the other poles simply by discarding their terms in the partial fraction expansion of FðsÞ. The purpose of this example is to examine a dominant pole approximation of the transform

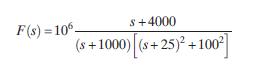
(a) Construct a partial-fraction expansion of FðsÞ and find f t ð Þ.

(b) Construct a pole-zero diagram of F s ð Þ and identify the dominant poles.

(c) Construct a dominant pole approximation gðtÞ by discarding the other poles in the partial fraction expansion in part (a).

(d) Plot f t ð Þ and g t ð Þ and comment on the accuracy of the approximation.

F(s)=106- S+4000 (s+1000) (s+25)2+1002