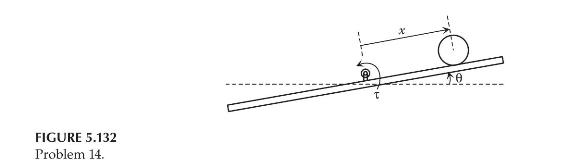
Consider the ball and beam system [10] shown in Figure 5.132, in which \(I\) and \(I_{\mathrm{b}}\) are the mass moments of inertia of the beam and the ball, respectively, \(m\) is the mass of the ball, and \(r\) is the radius of the ball. The beam is made to rotate in a vertical plane by applying a torque \(\tau\) at the center of rotation and the ball is free to roll (with one degree of freedom) along the beam. It is assumed that the ball remains in contact with the beam and that the rolling occurs without slipping. The system parameters are \(I=0.02 \mathrm{~kg} \cdot \mathrm{m}^{2}, I_{\mathrm{b}}=2 \times 10^{-6} \mathrm{~kg} \cdot \mathrm{m}^{2}, m=0.05 \mathrm{~kg}\), and \(r=0.01 \mathrm{~m}\).

a. Choosing the beam angle \(\theta\) and the ball position \(x\) as generalized coordinates, derive the nonlinear equations of motion of the system by using the Lagrange's equations.

b. Choosing \(\theta, \dot{\theta}, x\), and \(\dot{x}\) as state variables and \(\tau\) as the input, find the state variable equations of the nonlinear system.

c. Assuming small angular motion, find the state-space form for the linearized system (with \(\theta\) and \(x\) as outputs).

d. Build two Simulink block diagrams, one using the differential equations obtained in Part (a) and the other using the state-space form found in Part (c). Compare the beam angle \(\theta(t)\) and the ball displacement \(x(t)\) when the torque applied to the system is a pulse function, \(\tau(t)=1 \mathrm{Nm}\) for \(1 \leq t \leq 2 \mathrm{~s}\).

Transcribed Image Text:

FIGURE 5.132 Problem 14.