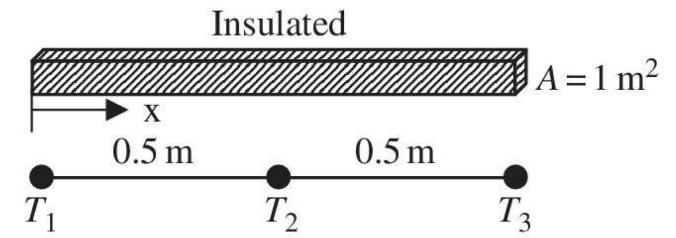
Question: In order to solve a 1D steadystate heat transfer problem, one element with 3nodes is used. The shape functions and the conductivity matrix before applying
In order to solve a 1D steadystate heat transfer problem, one element with 3nodes is used. The shape functions and the conductivity matrix before applying boundary conditions are given.
![N(x)=1-3x+2x N2(x)=4x-4x N3(x) = x+2x 1-21 , [K]=-24 -24-2 1-22](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1710/5/8/1/15565f565a33f5691710581155300.jpg)
a. When the temperature at node 1 is equal to \(50^{\circ} \mathrm{C}\) and a heat flux of \(80 \mathrm{~W}\) is provided at node 3 , calculate the temperature at \(x=1 / 4 \mathrm{~m}\).
b. When the temperature at node 1 is equal to \(50^{\circ} \mathrm{C}\) and the convection boundary condition is applied at node 3 with \(h=4 \mathrm{~W} / \mathrm{m}^{2} /{ }^{\circ} \mathrm{C}, T^{\infty}=120^{\circ} \mathrm{C}\), calculate the temperature at \(x=1 / 4 \mathrm{~m}\).
c. Instead of the previous boundary conditions, heat fluxes at nodes 1 and 3 are given as \(Q_{1}\) and \(Q_{3}\), respectively. Can this problem be solved for the nodal temperatures? Explain your answer.
N(x)=1-3x+2x N2(x)=4x-4x N3(x) = x+2x 1-21 , [K]=-24 -24-2 1-22
Step by Step Solution
3.53 Rating (153 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


