Repeat Problem 8.14 for the load shown in Example 8.4 (Figure 8.6).

Data From Problem 8.14:-

The voltages given in Problem 8.10 are applied to a balanced-Y load consisting of \((12+j 16)\) ohms per phase. The load neutral is solidly grounded. Draw the sequence networks and calculate \(I_{0}, I_{1}\), and \(I_{2}\), the sequence components of the line currents. Then calculate the line currents \(I_{a}, I_{b}\), and \(I_{c}\).

Data From Problem 8.10:-

Given the line-to-ground voltages \(V_{a g}=280 / 0^{\circ}, V_{b g}=250 \angle-110^{\circ}\), and \(V_{c g}=290 / 130^{\circ}\) volts, calculate (a) the sequence components of the line-to-ground voltages, denoted \(V_{\mathrm{L} g 0}, V_{\mathrm{L} g 1}\), and \(V_{\mathrm{L} g 2}\); (b) line-to-line voltages \(V_{a b}, V_{b c}\), and \(V_{c a}\); and (c) sequence components of the line-to-line voltages \(V_{\mathrm{LL} 0}, V_{\mathrm{LL} 1}\), and \(V_{\mathrm{LL} 2}\). Also, verify the following general relation: \(V_{\mathrm{LL} 0}=0, V_{\mathrm{LL} 1}=\sqrt{3} V_{\mathrm{L} g 1} /+30^{\circ}\), and \(V_{\mathrm{LL} 2}=\sqrt{3} V_{\mathrm{L} g 2} /-30^{\circ}\) volts.

Data From Example 8.4:-

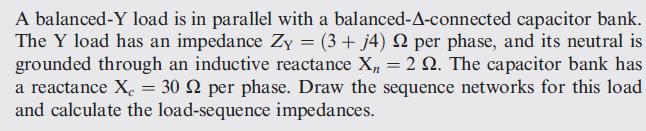
Figure 8.6:-

A balanced-Y load is in parallel with a balanced-A-connected capacitor bank. The Y load has an impedance Zy = (3+ j4) 2 per phase, and its neutral is grounded through an inductive reactance X = 22. The capacitor bank has a reactance X = 30 2 per phase. Draw the sequence networks for this load and calculate the load-sequence impedances.