Solve the differential equation in problem 8 for the following boundary conditions using the Galerkin method:

Assume the approximate solution as:

where \(\phi_{0}(x)\) is a function that satisfies the essential boundary conditions, and \(\phi_{1}(x)\) is the weight function that satisfies the homogeneous part of the essential boundary conditions, that is, \(\phi_{1}(0)=\phi_{1}(1)=0\). Hence, assume the functions as follows:

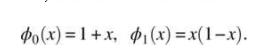
Compare the approximate solution with the exact solution by plotting their graphs. The exact solution can be derived as:

Data From Problem 8:

Consider the following differential equation:

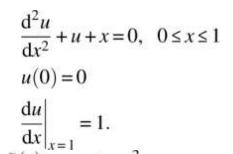
u(0)=1, u(1)=2.