The shape functions of a linear 3node element are also called barycentric or area coordinates because they uniquely define the location of a point in the triangle. Show that the shape functions in eq. (4.69) can also be computed as:

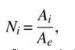
where \(A_{1}\) is the area of triangle \(\mathrm{P} 23\) in the figure, \(A_{2}\) is the area of triangle \(\mathrm{P} 13, A_{3}\) is the area of triangle P12, and \(A_{e}=A_{1}+A_{2}+A_{3}\) is the area of triangle 123 .

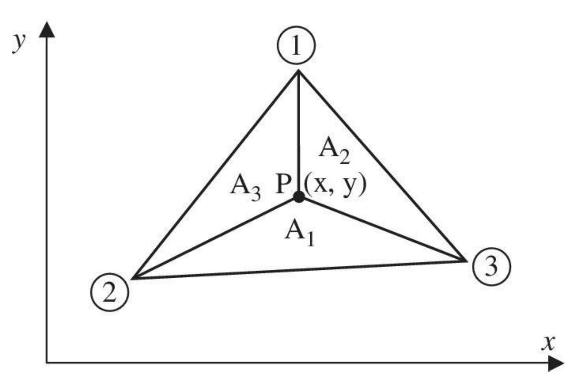
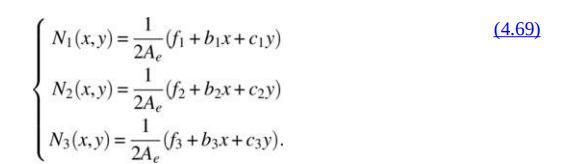
A N = Ae