Transform the system

\[\begin{aligned}& \underline{\dot{\mathbf{x}}}=\mathbf{A} \mathbf{x}+\mathbf{B u} \\& \mathbf{y}=\mathbf{C x}\end{aligned}\]

into observable canonical form, given that the system matrices are \[
\mathbf{A}=\left[\begin{array}{lll}
1 & 2 & 2 \\
1 & 4 & 3 \\
3 & 1 & 3 \end{array}ight] \quad \mathbf{B}=\left[\begin{array}{l}
1 \\
0 \\
1 \end{array}ight] \quad \mathbf{C}=\left[\begin{array}{lll}
2 & 1 & 1 \end{array}ight]
\]

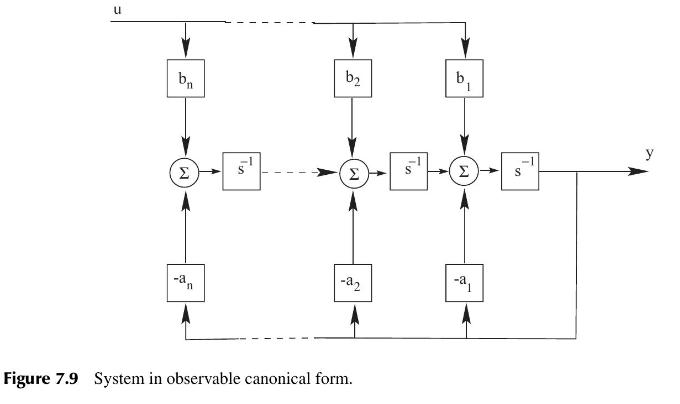
u bn 5 b b 1 S -a2 -a Figure 7.9 System in observable canonical form. S y