Question: For a, b, c three real numbers consider the system x + ax + ax + ax3 = a + bx + bx +

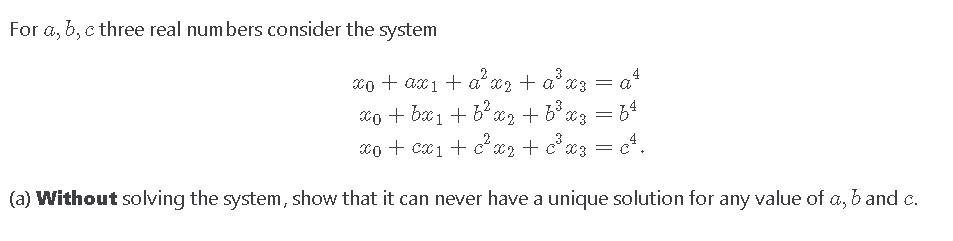
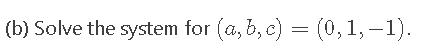
$For ( a, b, c ) three real num bers consider the system [ begin{aligned} x_{0}+a x_{1}+a^{2} x_{2}+a^{3} x_{3} & =a^{4}$ (b) Solve the system for ( (a, b, c)=(0,1,-1) ).

For a, b, c three real numbers consider the system x + ax + ax + ax3 = a + bx + bx + b x3 = 64 x + cx + x + c x3 = x (a) Without solving the system, show that it can never have a unique solution for any value of a, b and c. (b) Solve the system for (a, b, c) = (0, 1, -1).

Step by Step Solution

★★★★★

3.48 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To show that the system can never have a unique solution for any value of a b and c we can observe ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

Consider an American call option on a stock. The stock price is $70, the time to maturity is eight months, the risk-free rate of interest is 10% per annum, the exercise price is $65, and the...

Googles ease of use and superior search results have propelled the search engine to its num- ber one status, ousting the early dominance of competitors such as WebCrawler and Infos- eek. Even later...

How do acculturation, assimilation, and integration impact individual identity formation and development?

Comicdur the system described by Obtain the transfer function matrix of the system.5) Compute At for A = To I -2 - 3 using the following three methods: - a Direct series expansion of e At b eft = d [...

Please show work, and SKIP PAGES 17 THROUGH 19 MATH 080 Final-Exam Review Revised October 2018 Can you simplify an expression using the order of operations? 1) Simplify 2) Simplify A) 32(11 - 8) - 18...

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.6 Problems Find...

Can you please help me with number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Linear Systems quations 406 The...

Can you please help me with number 21. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Open with Chapter 5 Linear Systems...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

A ball is thrown upward from a height of 880 feet above the ground. with an initial velocity of 96 feet per second. From physics it is known that the velocity at time t is vft) = 96 32t feet per...

YOUR TASK As a Marketing Consultant, advice John Samson by preparing a strategic marketing plan to the Board to position HHRE as the market leader and a viable venture in the real estate business....

Question No. 4. A 5-star hotel has 200 rooms that has historically charged one set of prices for its room, which was Rs. 5000 per night. The variable cost for one room includes cleaning,...

Linux Systems Administration In this module's class activities, you acted as a system administrator in order to troubleshoot a malfunctioning Linux server. The senior administrator was quite pleased...

Draw the kinematic diagram of the following linkages and find their mobility using Gruebler's equation. 1 B 2 3 -O- D 6 C 4 Point C is not a joint. It is a significant point on link 5.

The Canadian Tire trying to expand into the USA Company: The Canadian Tire What are the sustainable strategic goals of the company? What aspects about the country could be good for the company on the...

The IRS assessed a $40,700 income tax deficiency plus $4,970 interest against Mr. and Mrs. Reczyk because of an alleged understatement of investment income. They refused to pay and took their case to...

A stock has had returns of 8 percent, 26 percent, 14 percent, 17 percent, 31 percent, and 1 percent over the last six years. What are the arithmetic and geometric average returns for the stock?

Consider a stock index currently standing at 250. The dividend yield on the index is 4% per annum, and the risk-free rate is 6% per annum. A three-month European call option on the index with a...

A futures price is currently $40. The risk-free interest rate is 5%. Some news is expected tomorrow that will cause the volatility over the next three months to be either 10% or 30%. There is a 60%...

A call with a strike price of $60 costs $6. A put with the same strike price and expiration date costs $4. Construct a table that shows the profit from a straddle. For what range of stock prices...

Explain in nontechnical terms why oligopolistic prices may tend to be inflexible.

How does economic rivalry take place in monopolistic competition? Describe the different aspects of product differentiation and price competition.

Why does the short-run marginal-cost curve eventually increase for the typical firm?