Determine matrix \(\mathbf{A}\) in the state equations \((\dot{\mathbf{X}}=\mathbf{A X}+\mathbf{B} u)\) for the block-diagram of Fig. 1.5 if \(\mathbf{X}=\left[\begin{array}{l}x_{1}(t) \\ x_{2}(t)\end{array}ight]\).

1) \(\left[\begin{array}{cc}0 & -\beta \\ 1 & -\alpha\end{array}ight]\)
2) \(\left[\begin{array}{cc}-\alpha & -\beta \\ 1 & 0\end{array}ight]\)
3) \(\left[\begin{array}{cc}0 & 1 \\ -\beta & -\alpha\end{array}ight]\)
4) \(\left[\begin{array}{ll}-\alpha & 1 \\ -\beta & 0\end{array}ight]\)

Figure 1.5

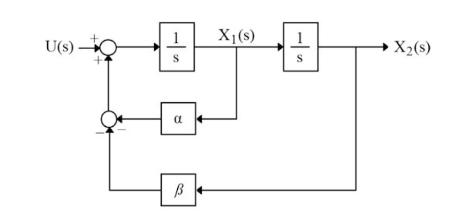
U(s)- S B 1 X2(s) X(s) S