Figure (mathrm{P}_{3}-80) displays two generalized interface circuit designs. In both circuits, resistors (R_{1}) and (R_{2}) connect a Thvenin equivalent circuit to a load resistor. Using

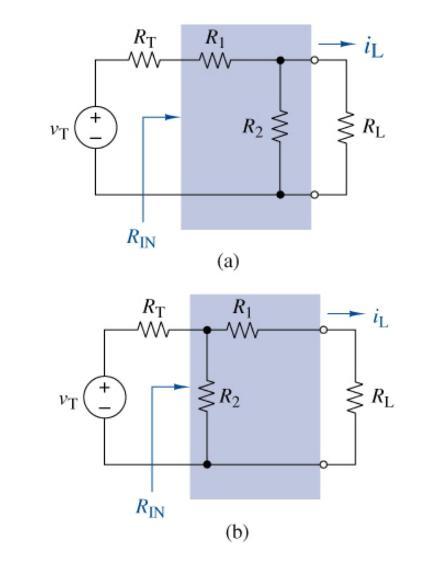
Figure \(\mathrm{P}_{3}-80\) displays two generalized interface circuit designs. In both circuits, resistors \(R_{1}\) and \(R_{2}\) connect a Thévenin equivalent circuit to a load resistor. Using MATLAB, develop symbolic expressions for the load current, \(i_{\mathrm{L}}\), and the input resistance, \(R_{\text {IN }}\), for each circuit in terms of the given parameters. Using these two expressions, now use the MATLAB command solve to solve for \(R_{1}\) and \(R_{2}\) in terms of \(i_{\mathrm{L}}\) and \(R_{\mathrm{IN}}\). Let \(v_{\mathrm{T}}=15 \mathrm{~V}, R_{\mathrm{T}}=100 \Omega, R_{\mathrm{L}}=50 \Omega, i_{\mathrm{L}}=50 \mathrm{~mA}\), and \(R_{\mathrm{IN}}=\) \(100 \Omega\). Can you use both types of interface circuits to find suitable values for \(R_{1}\) and \(R_{2}\) to meet these specifications? Compare your interface design(s) with the solution to Problem \(3^{-71 .}\)

VT VT RT ww RIN RT RIN R (a) R R ww R2 (b) ww ww iL RL iL RL