Question: Try to solve Problem 6.2 using the Jacobi and Gauss-Seidel iterative methods with the value of (mathrm{A}_{33}) changed from 14 to 0.14 and with (x_{1}(0)=x_{2}(0)=)

Try to solve Problem 6.2 using the Jacobi and Gauss-Seidel iterative methods with the value of $\mathrm{A}_{33}$ changed from 14 to 0.14 and with $x_{1}(0)=x_{2}(0)=$ $x_{3}(0)=0$. Show that neither method converges to the unique solution.

Problem 6.2

Using Gauss elimination and back substitution, solve

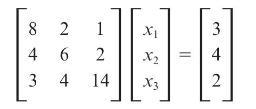
82 1 4 6 2 3 4 14 X X 3 4

82 1 4 6 2 3 4 14 X X 3 4 2

Step by Step Solution

★★★★★

3.37 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Systems Analysis Design Questions!

Q1. You have identified a market opportunity for home media players that would cater for older members of the population. Many older people have difficulty in understanding the operating principles...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

can someone solve this Modern workstations typically have memory systems that incorporate two or three levels of caching. Explain why they are designed like this. [4 marks] In order to investigate...

EFB106 COST AND BENEFIT ANALYSIS FOR PROJECT APPRAISAL Assessment Item 1: Sensitivity Analysis Online resource: http://www.cbabuilder.co.uk/ CBA Builder Excel Tool:...

Assignment 1 1. Food A contains 20 units of vitamin x and 40 units of vitamin y per gram. Food B contains 30 units of each of vitamins x and y. The daily minimum human requirements of vitamin x and y...

Solve the linear programming problems by drawing the feasible solution region and using the corner point table. 1.1 Maximize: P = 20x + 10y subject to: 3x + y 21 x + y 9 x + 3y 21 x, y 0 1 .2...

SAMPLING MEAN: DEFINITION: The term sampling mean is a statistical term used to describe the properties of statistical distributions. In statistical terms, the sample mean from a group of...

Looking for assistance in Finance HW..... I ONLY Need the FORMULASin the function ribbon (for the answers that I already have, which are attached below) Please advise if you can assist and provide...

Math 400 Assignment #3 -- Numerical Integration and Differentiation 1. For the function g x e x 2 2 Due: 6am April 09, 2016 use the centered difference formula with h 101 , 102 , , 1020 to create a...

9/14/10 12:39 PM Page 381 Chapter dug84356_ch06a.qxd 6 Rational Expressions Advanced technical developments have made sports equipment faster, lighter, and more responsive to the human body. Behind...

A charge 4q is at a distance r from a charge "q. Compare the number of electric field lines leaving the charge 4q with the number entering the charge "q. Where do the extra lines beginning on 4q end?

Look again at the project cash flows in Practice Question 6. Calculate the modified IRR as defined in footnote 5 in Section 5.3. Assume the cost of capital is 12 percent. Now try the following...

On April 2 , Kelvin sold $ 4 0 , 0 0 0 of inventory items on credit with the terms 1 / 1 0 , n / 3 0 . If net method was used to record the sales discounts ( i . e . cash discounts ) , Kelvin should...

=6. What quantities appear in the forecast cells of the spreadsheet model for this problem?

Consider the circuit shown in Figure. The parameter values are R = 103 , C = 2 x 10-6 F, and L = 2 x 10-3 H. The voltage v1 is a step input of magnitude 5 V, and the voltage v2 is sinusoidal with...

The block diagram of a machine-tool control system is shown in Figure AP4.8. (a) Determine the transfer function T(s) =Y(s)/R(s). (b) Determine the sensitivity STb. (c) Select K when 1 ¤ K...

Designers have developed small, fast, vertical-takeoff fighter aircraft that are invisible to radar (stealth aircraft). This aircraft concept uses quickly turning jet nozzles to steer the airplane...

Oh my gosh. These bonds confuse me. Tell me everything you know about bonds

1. Father owns land which he purchased sevarl years ago for 80,000. It has current FMV of 90,000. Father leases land on ten year lease and is paid 6,000 of rent each year, semi-annually April 1st and...

During 2017, Martinez Company started a construction job with a contract price of $1,580,000. The job was completed in 2019. The following information is available. 2017 2018 2019 Costs incurred to...