Calculation problem: Testing the null hypothesis that the slope equals zero. Can the relationship be explained by sampling error? Using the face ratio and hockey penalty data from Practice Problem 1, test the null hypothesis that the slope of the regression line is zero.

a. State the null and alternate hypotheses.

b. What is β₀ for this null hypothesis?

c. Calculate the test statistic t from b , β₀ , and the standard error of b.

d. Find the critical value of t appropriate for the degrees of freedom, at α=0.05.

e. Is the absolute value of the t for this test greater than the critical value?

f. Using a computer or the statistical tables, be as precise as possible about the P-value for this test. Draw conclusions from the test.

g. What fraction of the variation in average penalty minutes per game is accounted for by face ratio?

Calculate the value of R^2.

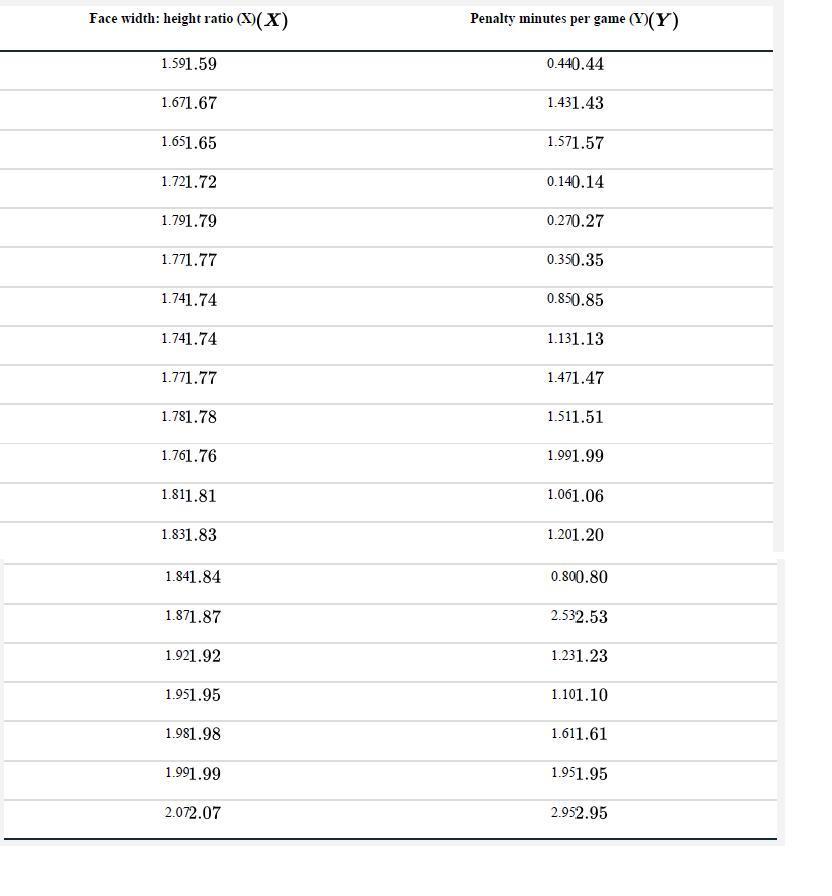
Data from Practice Problem 1,

Calculation problem: Regression lines. Men’s faces have higher width-to-height ratios than women’s, on average. This turns out to reflect a difference in testosterone expression during puberty. Testosterone is also known to predict aggressive behavior. Does face shape predict aggression? To test this, Carré and McCormick (2008) compared the face width-to-height ratio of 21 university hockey players with the average number of penalty minutes awarded per game for aggressive infractions like fighting or cross-checking. Their data are below along with some partial calculations. We will calculate the equation for the line that best predicts penalty minutes from face width-to-height ratio.