Outliers can occur in a sample of data for several reasons, including instrument failure, measurement error, and real variation in the population. The “trimmed mean” is a method developed for estimating a population mean when a measurement is prone to producing outliers. A trimmed mean is an ordinary sample mean calculated on data after the most extreme measurements have been dropped according to a percentile criterion. A 5% trimmed mean drops the measurements below the 5th percentile (0.05 quantile) and above the 95th percentile. In 1882, Simon Newcomb estimated the speed of light by measuring the time it took for light to return to his lab after being bounced off a mirror, a round trip of 7442 meters. The following is the frequency distribution of 66 measurements Newcomb made of this time, in microseconds (i.e., in millionths of a second) (Stigler 1977).

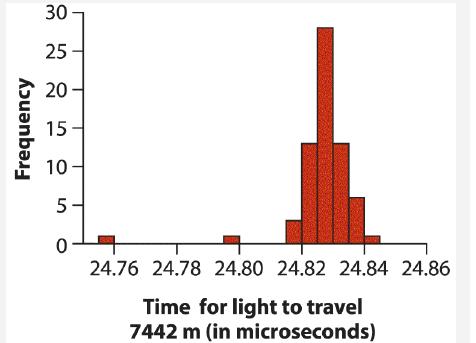
The distribution includes outliers, and the trimmed mean is an objective way to increase the precision of the estimate. For the light data, the 5% trimmed mean drops the three smallest and three largest values, yielding the value 24.8274 for the mean of the remaining measurements. Bootstrapping is an excellent way to calculate the uncertainty of the trimmed mean. The results of 1000 bootstrap replicate estimates of the trimmed mean are shown in the following histogram. Of the bootstrap estimates, 2.5% were below 24.8254, 5% were below 24.8260, 95% were below 24.8285, and 97.5% were below 24.8288.

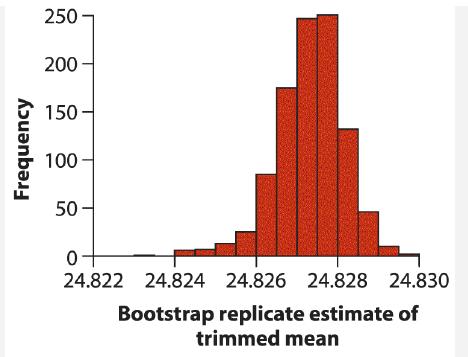
a. Calculate a 95% confidence interval for the trimmed mean.

b. The ordinary, “untrimmed” mean of the 66 data points, including the outliers, is 24.8262. Is the ordinary sample mean contained in the 95% confidence interval for the trimmed mean?