It was asserted that in order for entropy to be an extensive quantity, the classical partition function of a system of indistinguishable particles must be divided by N!. Consider a box evenly partitioned into two halves, each with volume V, and each containing N atoms of a monatomic ideal gas at a temperature T. Compute the entropy from eq.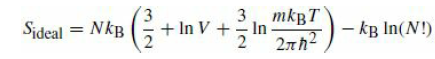 
omitting the last term. Now remove the partition, and compute the entropy of the resulting system of 2N particles in a volume 2V again from eq.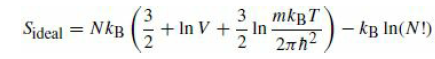 

with the last term omitted. We have not lost any information about the system, but the entropy seems to have increased if we compute it without the Gibbs factor! Next, restore the N! factor and repeat the analysis.

3 mkBT In 2nh2 Sideal = NkB 3. + In V + kg In(N!) Sideal = NkB 3. + In V + 3 mkBT In 2nh2 kg In(N!)