Consider the following algorithm for generating a random permutation of the elements 1, 2, . . . , n. In this algorithm, P(i) can be interpreted as the element in position i.

Step 1: Set k = 1.

Step 2: Set P(1) = 1.

Step 3: If k = n, stop. Otherwise, let k = k +1.

Step 4: Generate a random number U, and let

(a) Explain in words what the algorithm is doing.

(b) Show that at iteration k—that is, when the value of P(k) is initially set—
that P(1),P(2), . . . , P (k) is a random permutation of 1, 2, . . . , k.
Hint: Use induction and argue that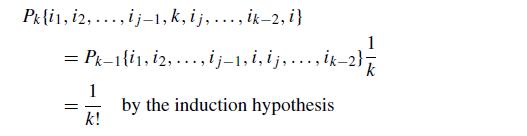

The preceding algorithm can be used even if n is not initially known.
22. Verify that if we use the hazard rate approach to simulate the event times of a nonhomogeneous Poisson process whose intensity function λ(t) is such that λ(t) ≤ λ, then we end up with the approach given in method 1 of Section 11.5.

P(k) = P([kU]+1), P([kU]+1)=k. Go to step 3.