Prove that the function defined by the equations

\[ f(t)=f(-t), \quad f(t+2 a)=f(t), \quad f(t)=\frac{a-t}{a} \text { for } 0 \leqslant t \leqslant a \]

is a characteristic function.

The characteristic functions of Examples 2 (d) and 5 possess the following remarkable property:

\[ \begin{gathered} f_{2}(t)=f_{5}(t) \text { for }|t| \leqslant a \\ f_{2}(t) eq f_{5}(t) \text { for }|t|>a \text { and } t eq \pm 2 a, \ldots \end{gathered} \]

There, thus, exist characteristic functions whose values coincide in an arbitrarily large interval \((-a,+a)\) and are not identically equal. The first instance of two such characteristic functions was pointed out by B. V. Gnedenko; then Krein indicated the necessary and sufficient conditions for which the identity of two characteristic functions follows from their equality in some interval \((-a,+a)\).

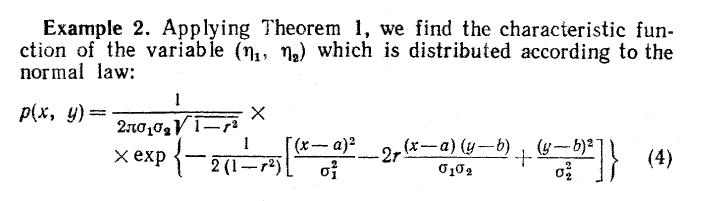
Example 2. Applying Theorem 1, we find the characteristic fun- ction of the variable (n, n) which is distributed according to the normal law: 1 p(x, y)= 2010,VT x exp | -2 (1- [(x-a) - 72) -2(x-a) (yb) (y-b)21 + (4) 0102