(a) A particle in a box has wave function ­Ï(x, t) = Ï 2 (x)e -iE2t/ ,...

(a) A particle in a box has wave function ­Ïˆ(x, t) = ψ₂(x)e^-iE2t/„, where ψ_nand E_nare given by Eqs. (40.35) and (40.31), respectively. If the energy of the particle is measured, what is the result?

(b) If instead the particle has wave function ψ(x, t) = (1/ˆš2)(ψ₁(x)e^-iE1t/„ + ψ₂(x)e^-iE2t/„) and the energy of the particle is measured, what is the result?

(c) If we had many identical particles with the wave function of part (b) and measured the energy of each, what would be the average value of all of the measurements? Can we say that, before the measurement was made, each particle had this average energy? Explain.

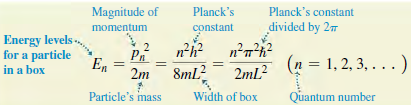
Eq.40.31

Eq.40.35

Transcribed Image Text:

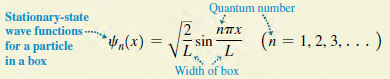
Magnitude of Planck's Planck's constant divided by 27 Energy levels- for a particle momentum constant nh? Pn 8mL? 2m n²m²h? 2mL? En = (n = 1, 2, 3, ...) in a box Quantum number Particle's mass Width of box Quantum number Stationary-state wave functions for a particle in a box 2 (x)"h, *Vn(x) (n = 1, 2, 3, . . . ) sin Width of box