Suppose that we wish to multiply two very large numbers (possibly thousands of bits long) on a 16-bit computer. In this problem, we will investigate a technique for doing these using FFTs.

(a) Let p(x) and q(x) be the two polynomials, show that the coefficients of the polynomial r(x) = p(x) q(x) can be computed using circular convolution.

(b) Show how to computer the coefficients of r (x) using a radix -2 FFT program. For what orders of magnitude of (L + M) is this procedure more efficient than direct computation? Assume that L + M =2^v for some integer v.

(c) Now suppose that we wish to compute the product of two very long positive binary integers u and v. Show that their product can be computed using polynomial multiplication, and describe an algorithm for computing the product using an FFT algorithm. If u is an 8000-bit number and v is a 1000-bit number, approximately how many real multiplications and additions are required to compute the product u . v using this method?

(d) Give a qualitative discussion of the effect of finite-precision arithmetic in implementing the algorithm of part (c).

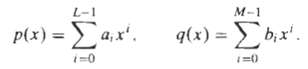
M-1 L-1 - 9() %3D ,. p(x) = a,x'. i=0