Suppose the current density changes slowly enough that we can (to good approximation) ignore all higher derivatives in the Taylor expansion J(tr) = J(t) + (tr ?? t) J (t) +... (for clarity, I suppress the r-dependence, which is not at issue). Show that a fortuitous cancellation in Eq. 10.31 yields That is: the Biot-Savart law holds, with J evaluated at the non-retarded time. This means that the quasistatic approximation is actually much better than we had any right to expect: the two errors involved (neglecting retardation and dropping the second term in Eq. 10.31) cancel one another, to first order.

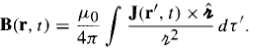
J(r', 1) x B(r, 1) = fr',! 22 P40 47 -dt'.