Suppose that x_c(t) is a continuuous-time stationary random signal with autocorrelation function

?_c(?) = ?{x_c(t)x_c(t + ?)}

and power density spectrum

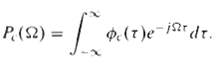
Consider a discrete-time stationary random signal x[n] that is obtained by sampling x_c(t) with sampling period T; i.e., x[n] = x_c(nT).

(a) Show that ?[m], the autocorrelation sequence for x[n], is?

?[m] = ?_c(mT).

(b) What is the relationship between the power density spectrum Pc(?) for the continuous-time random signal and the power density spectrum P(?) for the discrete-time random signal?

(c) What condition is necessary such that?

P(?) = 1/T P_c (?/T) . ? ? ? ? ? ? ? |?|

2P 131 -3( 2)'$ P.(2) =