The question has been raised whether an open-loop unstable process can be stabilized with a proportional-only controller.

(a) For the process and controller shown in figure a, find the range of Kc values that yield a stable response. (Note that τ is positive.)

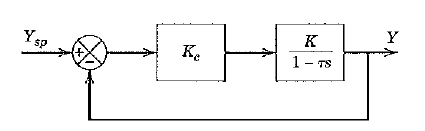
(b) Check the gain of Y(s)/Y_sp (s) to make sure that the process responds in the correct direction if K is within the range of part (a).

(c) For K = 10 and τ = 20, find the value of K_c that yields a pole at s = – 0.1. What is the offset for these conditions?

(d) Suppose that you had designed the controller neglecting a second smaller time constant. Would the controller still yield a stable closed-loop response? To check the “robustness” of your design, find the general conditions on K_c and τ_m for stability if the system is as shown in Figure. Are these conditions generally easy (or difficult) to meet? Explain. Show for τ_m = 5, that your value of K_c from part (c) does/does not still yield a stable system.

Y39 K. 1- TS