There are important applications in which due to known scientific constraints, the regression line must go through the origin (i.e., the intercept must be zero). In other words, the model should read, and only a simple parameter requires estimation. The model is often called the regression through the origin model.

(a) Show that the least squares estimator of the slope is

(b) Show that

(c) Show that 6 in part (a) is an unbiased estimator for 0. That is, show E (B) =3.

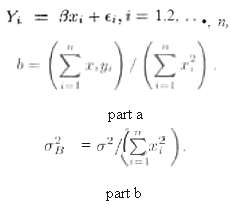
Y. = Ba, + 6;, i = 1.2. %3D (E-m) (E-) part a =o*/C# ). part b