This exercise is based on results in Brewer and Donadio (2003).

a Show, using the results in Theorem 6.1, that the variance in (6.21) can be rewritten as:

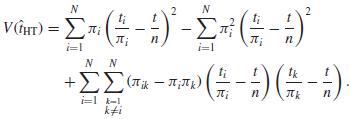
Write t _i / π_i − t_k / π_k = t_i / π_i – t / n + t / n − t_k / π_k .

b The first term in (6.47) is the variance that would result if a with replacement sample with selection probabilities ψ_i = π_i / n were taken. Brewer and Donadio (2003) suggest that the second term may be viewed as a finite population correction for unequal-probability sampling, so that the first two terms in (6.47) approximate V(ṫ_HT) without depending on the joint inclusion probabilities π_ik . Calculate the three terms in (6.47) for an SRS of size n.

c Suppose that there exist constants c_i such that π_ik ≈ π_iπ_k(c_i + c_k)/2. Show that with this substitution, the third term in (6.47) can be approximated by

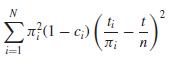
so that

Two choices suggested for c_i are c_i = (n −1) / (n −π_i) or (following Hartley and

Rao, 1962),

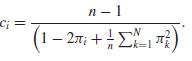
Calculate the variance approximation in (6.48) for an SRS with each of these choices of c_i.

! +(".-"m@-:):)