We can extend our growth-accounting equation to include three factors and write the following equation: where g Q = the
Question:
We can extend our growth-accounting equation to include three factors and write the following equation:
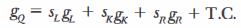
where gQ = the growth rate of output, gi = the growth rate of inputs (i = inputs to production: L for labor, K for capital, and R for land and other natural resources), and si = the contribution of each input to output growth as measured by its share of national income (0 ≤ si ≤ 1 and sL + sK + sn = 1 ) . T.C. measures technological change.
a. In the poorest developing countries, the share of capital is close to zero, the main resource is agricultural land (which is constant), and there is little technological change. Can you use this to explain the
Malthusian hypothesis in which per capita output is likely to be stagnant or even to decline (i.e., gQ < g)?
b. In advanced economies, the share ofland resources drops to virtually zero. Why does this lead to the growth-accounting equation studied in the previous chapter? Can you use this to explain how countries can avoid the Malthusian trap of stagnant incomes?
c. According to economists who are pessimistic about future prospects (including a group of ne Malthusians from the Club of Rome), T.C. is close to zero, the available supply of natural resources is declining, and the share of resources is large and rising. Does this explain why the future of industrial societies might be bleak? Which assumptions of the neo-Malthusians might you question?
This problem has been solved!
Step by Step Answer:
a Let s k g k T C 0 Then g Q s L g L g L as long as sL 1 as can be …View the full answer
