Question: We know that one solution of the basic spring equation in Exercise 15 is x(t) = cos(t). Find v(t) and check that the solution matches

We know that one solution of the basic spring equation in Exercise 15 is x(t) = cos(t). Find v(t) and check that the solution matches the system of equations. What are the initial position and velocity?

The spring equation or simple harmonic oscillator

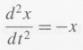
dex dr?

studied in Subsection 2.10.3 describes how acceleration (the second derivative of the position x) is equal to the negative of the position. The spring constant k has been set to 1 for simplicity. This one equation for the second derivative can be written as a system of two autonomous differential equations.

dex dr?

Step by Step Solution

★★★★★

3.36 Rating (165 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

vt sint d x dt and dvdt ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

808-C-D-E (1118).docx

120 KBs Word File

Students Have Also Explored These Related Calculus Questions!

One solution of the spring equation with friction in Exercise 16 is x(t) = e t cos(t). Find v(t) and check that the solution matches the system of equations. What are the initial position and...

If we have 20 pairs of sample data with a correlation coefficient of 1, then we know that one of the two variables is definitely the cause of the other. Decide whether the statement make sense or...

Determine by inspection at least one solution of the given differential equation. 1. y'' = y' 2. y' = y(y 3)

AA210 HOMEWORK 1 SOLUTION 2015-2016 Spring September 30, 2015 Problem 1.2 (10 points) Assumptions: steady, incompressible, 2D flow Under the assumptions, we can relate velocity to the streamline...

I need the answer asap but the answer must be sure to get the perfect score for this, i need it typewritten. Please double check answer before submitting. Solve the following system of equations. V=...

All the information are in it (i) g(x) = x?(x + 5)%(x 1)(x 4) (a) Degree: ; Leading coefficient: ; based on this the end behavior is: (b) the x-intercepts: X-intercept Multiplicity Bounce or cross?...

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.6 Problems Find...

Can you please help me with number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Linear Systems quations 406 The...

Can you please help me with number 21. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Open with Chapter 5 Linear Systems...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

If the half-life of tritium (hydrogen-3) is 12.3 y, how much of a 0.00444 g sample of tritium is present after 5.0 y? After 250.0 y?

An experiment has 10 equally likely outcomes. Let A and B be two non-empty events of the experiment. If A consists of 4 outcomes, then the number of outcomes that B must have, so that A and B are...

Mr . E donated stock, which he had held for 1 0 months, to his church. The stock had a fair market value of $ 1 , 0 0 0 at the time of the gift, but had only cost Mr . E $ 8 0 0 . What amount can he...

Treating drunk drivers. Once a person has been convicted of drunk driving, one purpose of court-mandated treatment or punishment is to prevent future offenses of the same kind. Suggest three...

Following are two confidence interval estimates of the mean of the cycles to failure of an automotive door latch mechanism (the test was conducted at an elevated stress level to accelerate the...

n = 100 random samples of water from a fresh water lake were taken and the calcium concentration (milligrams per liter) measured. A 95% CI on the mean calcium concentration is 0.49

The breaking strength of yarn used in manufacturing drapery material is required to be at least 100 psi. Past experience has indicated that breaking strength is normally distributed and that = 2 psi....

Compute return on investment for each of the divisions below (each is an investment center). Which division performed the best, based on return on investment? Complete this question by entering your...

A research center claims that 31% of adults in a certain country would travel into space on a commercial flight if they could afford it. In a random sample of 700 adults in that country, 35% say that...

You sampled 50 students at Rutgers University-Camden and calculated the mean number of hours spent studying during finals week to be 12. You also calculated a 95% confidence interval for the mean...