Question: With reference to Definition 4.4, show that 0 = 1 and that 1 = 0 for any random variable for which E(X) exists.

With reference to Definition 4.4, show that µ0 = 1 and that µ1 = 0 for any random variable for which E(X) exists.

Definition 4.4

The rth moment about the mean of a random variable X, denoted by µr, is the expected value of ( X – µ)r, symbolically

4, = E[(X-uY] = Ea-u f)

For r = 0, 1, 2, . . . , when X is discrete, and

When X is continuous.

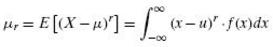
4, = E[(X-uY] = Ea-u f)

Step by Step Solution

★★★★★

3.20 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

H fx fx d... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Document Format (1 attachment)

Word file Icon

583-S-J-P-D (712).docx

120 KBs Word File

Students Have Also Explored These Related Statistics Questions!

Q:

Show that if 1

Q:

With reference to the generalized definition of binomial coefficients in Exercise 1.19, show that (a) (b) -l r) = (1)r (n+r-1 for n>0

Q:

With reference to Exercise 5.12, find the factorial momentgenerating function of (a) The Bernoulli distribution and show that µ'(1) = . and µ'(r) = 0 for r > 1; (b) The binomial...

Q:

1 1. It is thought that prehistoric Indians did not take their best tools, pottery, and household items when they visited higher elevations for their summer camps. It is hypothesized that...

Q:

8.5.7 Let X be a random variable with E ( X ) = p,Var(X) = a' and such that the third central moment 7 3 = E ( X - p)3 exists. The ratio 73/a3 is called the coeficient of skewness. Find skewness of...

Q:

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Q:

ductory Statistics Third Edition Perdisco Assessment Below is a set of assessable homework questions on this topic, selected by your professor. Take care! Do not submit your answers until you have...

Q:

4.4 Understanding the Principles 4.1 4.2 What is a random variable? How do discrete and continuous random variables differ? Applying the Concepts Basic 4.3 4.4 4.5 4.6 Type of Random Variable....

Q:

The unit circle {(x, y) : x2 +y2 = 1} is divided into three arcs by choosing three random points A, B, C on the circle (independently and uniformly), forming arcs between A and B, between A and C,...

Q:

Please fill out Part 1-4 yellow cells and please put equations and cell numbers AutoSave OFF BESU- Uoft Finance - Saved to my Mac Home Insert Draw Page Layout Formulas Data Review View Tell me Share...

Q:

Georgia Gould Bikes Inc. is in the process of setting a target price on its newly designed mountain bike. Cost data relating to the bike at a budgeted volume of 20,000 units are as follows. Georgia...

Q:

Suppose selected comparative statement data for the giant bookseller Barnes & Noble are presented here. All balance sheet data are as of the end of the fiscal year (in millions). Instructions Compute...

Q:

which bond will usually pay a higher interest rate aaa or bbb

Q:

The same principles should apply to the finances of the nation and to the finances of each individual or family.

Q:

The Georgetown, South Carolina, Traffic Division reported 40% of high-speed chases involving automobiles result in a minor or major accident. During a month in which 50 high-speed chases occur, what...

Q:

Cruise ships of the Royal Viking line report that 80% of their rooms are occupied during September. For a cruise ship having 800 rooms, what is the probability that 665 or more are occupied in...

Q:

The goal at U.S. airports handling international flights is to clear these flights within 45 minutes. Lets interpret this to mean that 95% of the flights are cleared in 45 minutes, so 5% of the...

Q:

2/2 Meredith has a loan amount of $126,600. She originated this loan by putting 5% down. What was be Meredith's original sales price? *

Q:

please help, thank you! 1) Suppose that today (12/9/21) you simultaneously enter 2 positions, both with the S&P 500 index as the underlying asset and with maturities on 6/17/2022. The first is a...

Q:

For each of the following problems, identity all valties used on your caleulator. Place the word SOLVE in the blank for the variable for which you need to solve. Then give the answer in the open...