With reference to Example 9.7, show that if the losses are proportional to the squared errors instead of their absolute values, the risk function becomes

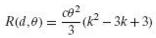
And its minimum is at k = 3/2.

Example 9.7

A random variable has the uniform density

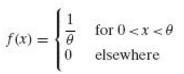
And we want to estimate the parameter θ (the “move” of Nature) on the basis of a single observation. If the decision function is to be of the form d(x) = kx, where k ≥ 1, and the losses are proportional to the absolute value of the errors, that is, 

L(kx,θ) = c|kx – θ|

Where c is a positive constant, find the value of k that will minimize the risk.

ce12 a)for 0