A capacitor C has been charged up to potential V0; at time t = 0 it is
Question:
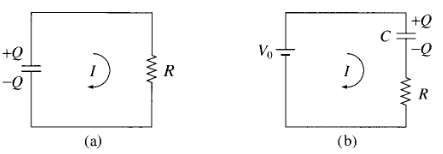
A capacitor C has been charged up to potential V0; at time t = 0 it is connected to a resistor R, and begins to discharge (Fig. 7.5a).
(a) Determine the charge 0n the capacitor as a function of time, Q(t). What is the current through the resistor, I(t)?
(b) What was the original energy stored in the capacitor (Eq. 2.55)? By integrating Eq. 7.7, confirm that the heat delivered to the resistor is equal to the energy lost by the capacitor. Now imagine charging up the capacitor, by connecting it (and the resistor) to a battery of fixed voltage V0, at time t: 0 (Fig. 7.5b).
(c) Again, determine Q(t) and I (t).
(d) Find the total energy output of the battery (f V0I dt). Determine the heat delivered to the resistor. What is the final energy stored in the capacitor? What fraction of the work done by the battery shows up as energy in the capacitor?
Step by Step Answer:
a VQC IR Because positive I means the charge on the capacitor is decreasi...View the full answer
