A batch reactor converts component A into B, which in turn decomposes into C: The concentrations of A and B are denoted by x1 and x2, respectively. The reactor model is: Thus, the ultimate values of x1 and x2 depend on the reactor temperature a function of time. For Find the constant temperature that maximizes the amount of B, for 0 ? t ? 8 min. Also allow the temperature to change as a cubic function of time. Find the values of a0, a1, a2, a3 that maximize x2 by using MATLAB to integrate the model and a suitable optimization method.

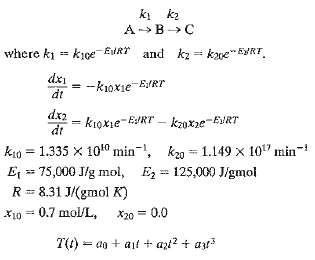
k k2 A B>C kz = kne" ERT. where kj = kjce EtRT and dxi = -k1oxie-E/RT dt dx2 kIoxie-ERT kzoxze-ERT dt k2g = 1.149 x 10" min- kio = 1.335 x 10to min-, E = 75,000 J/g mnol, Ez= 125,000 J/gmol 8.31 J/(gmol K) R X10 = 0.7 mol/L, X20 = 0.0 T(t) = an + ajf + azi? + ar?