(a) Prove that the average magnetic field, over a sphere of radius R, due to steady currents within the sphere, is where m is the total dipole moment of the sphere. Contrast the electrostatic result, Eq. 3.105.

[This is tough, so I'll give you a start: Write B as (V x A), and apply Prob. 1.60b. Now put in Eq. 5.63, and do the surface integral first, showing that (see Fig. 5.65). Use Eq. 5.91, if you like.]

(b) Show that the average magnetic field due to steady currents outside the sphere is the same as the field they produce at the center.

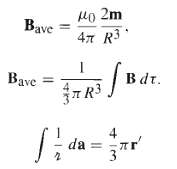
Bave Bave M40 2m 47 R3 I fBdr. R 1 1/2 d da = 413 4