(a) Show that

,

in S1 units for B_c- Because B_c decreases with increasing temperature, the right side is negative. The superconducting phase has the lower entropy: it is the more ordered phase. As τ → 0, the entropy in both phases will go to zero, consistent with the third law.  What does this imply for the shape of the curve of B_c versus τ?

(b) At τ = τ_c, we have B_c = 0 and hence σs = σ_N. Show that this result has the following consequences: (1) The two free energy curves do not cross at τ_c but merge, as shown in Figure (2) The two energies are the same: Us(τ_c) = U_N(τ_c). (3) There is no latent heat associated with the transition at τ = τ_c. What is the latent heat of the transition when carried out in a magnetic field, at τ < τ_c?

(c) Show that C_S and C_N, the heat capacities per unit volume, are related by

Figure 8.18 is a plot of C/T vs T² and shows that C_S decreases much faster than linearly with decreasing τ, while C_N decreases as Tτ. For τ << τ_c, ∆C is dominated by C_N. Show that this implies

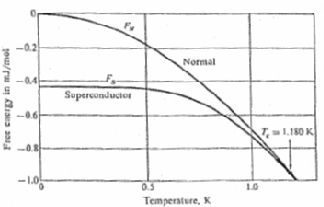
Experimental values of the free energy as a function of temperature for aluminum in the superconducting state and in the normal state. Below the transition temperature T_c = 1.180 K the free energy is lower in the superconducting state. The two curves merge at the transition temperature, so that the phase transition is second order (there is no latent heat of transition at T_c). The curve F_S is measured in zero magnetic field, and F_N is measured in a magnetic field sufficient to put the specimen in the normal state. Courtesy of N.E. Phillips.

Transcribed Image Text:

1 d(B?) (os-ON) Be dBc Ho dt 2Ho dt dt